But officer, the light was doppler-shifted to green

Most of the major intersections we pass through in Doha are roundabouts, in which otherwise normal drivers are transformed into complete maniacs. For better or worse, though, they (the roundabouts, not the drivers) are very good at making traffic flow more efficiently than signaled intersections. However, there are still a lot of traffic light intersections, as well as "controlled" roundabouts in which traffic lights direct the flow of cars through the roundabout (the latter combines the worst of both worlds, and I don't understand why they even need to exist). Some of these lights stay red for an unusually long time, which makes it just a little frustrating to wait at those intersections.

There's a way around this that was mentioned the other day: if you're driving fast enough, the red light will look green to you. Most people are familiar with the Doppler effect for sound waves, whether or not they know it by name: a siren traveling toward you will sound higher in pitch than one standing still with you, and in turn, a siren traveling away from you will sound lower in pitch. The same is true for light waves, but you need to use special relativity to describe it since light travels at the same speed no matter how fast you're going (sound travels at the speed of sound, but only relative to the air itself). If you're driving toward a light, you'll see it as a shorter wavelength ("blue-shifted," but not necessarily blue) than if you were just standing still with the light.

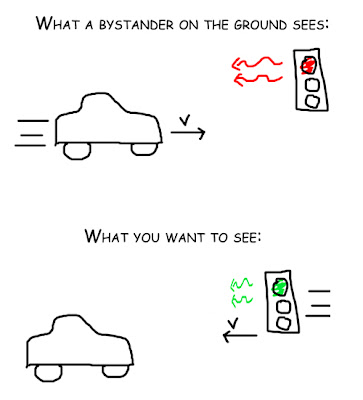
So the question is how fast you have to go for a red light to look like a green one. This is a problem you'd typically get in a special relativity class, but I'd forgotten the answer for some time so here is the calculation. If the traffic light is normally shining red, and you're speeding toward it at a velocity $$v$$, then the wavelength of light you see changes according to the equation (derivation, if interested)

\[\lambda_{obs} = \lambda_{red} \sqrt{ \frac{1 - v/c}{1 + v/c} } .\]
where $\lambda_{obs}$ is the wavelength of light that you observe from your speeding car, $\lambda_{red}$ is the wavelength of the red light, and $c$ is the speed of light (300 million meters per second). Rewriting the equation gives you

\[v = c \left( \frac{\lambda_{red}^2 - \lambda_{obs}^2}{\lambda_{red}^2 + \lambda_{obs}^2} \right) .\]
Red light has a wavelength ($\lambda_{red}$) of about 650 nm, and green light has a wavelength ($\lambda_{obs}$) of about 550 nm. Plug everything in and you get

\[v = \frac{24}{145} c \approx \frac{1}{6} c . \]
So you'd have to be driving at one-sixth the speed of light, or 50 million meters per second, or over 100 million mph. In one second, you'd encircle the Earth once and then some. But assuming you could push your car that fast, you could run a red light and legitimately tell the cops that it looked green to you.

Then again, they'd probably have a hard time catching you anyway. Plus, the actual green lights would look blue, which would just be really weird.